码龙的成长之路

0%

剑指offer

发表于 更新于
本文字数： 17k 阅读时长 ≈ 16 分钟

手撕代码系列之剑指offer中的典型题目

[toc]

1 数组中重复的数字(03)

在一个长度为 n 的数组 nums 里的所有数字都在 0～n-1 的范围内。数组中某些数字是重复的，但不知道有几个数字重复了，也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。

1
/** 输入：[2, 3, 1, 0, 2, 5, 3]
2
输出：2 或 3 
3
**/
4
class Solution {
5
    //nums[index]==num[nums[index]]
6
    //要求index位置的值nums[index]满足nums[index]==index
7
    public int findRepeatNumber(int[] nums) {
8
        for(int i=0;i<nums.length;i++){
9
            while(i!=nums[i]){//当第i个位置的值不等于i时
10
                //如: 3 2 1 3 0 2 5 3 nums[0]=3,nums[nums[0]]=nums[3]=3
11
                if(nums[i]==nums[nums[i]])//如果第i位置的值与第nums[i]个位置的值相等，即重复值
12
                    return nums[i];
13
                int temp = nums[i];
14
                nums[i]=nums[temp];
15
                nums[temp]=temp;
16
            }
17
        }
18
        return 0;
19
    }
20
}
21
//也可以利用HashSet存入每个数组元素的值，判断插入成功与否(if(!set.add(nums[i])))

2 二维数组的查找(04)

在一个 n * m 的二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

1
/** Input:[ [1,   4,  7, 11, 15], [2,   5,  8, 12, 19],
2
		   [3,   6,  9, 16, 22],[10, 13, 14, 17, 24],
3
		   [18, 21, 23, 26, 30]] 		 target=5,40
4
	OutPut:true,false
5
**/
6
public boolean findNumberIn2DArray(int[][] matrix, int target) {
7
    //类似于二分查找，从右上角开始查询
8
    if(matrix.length==0)
9
        return false;
10
    int row=  matrix.length,col = matrix[0].length;
11
    int i = 0,j=col-1;
12
    while(i<row&&j>=0){
13
        if(matrix[i][j]==target)
14
            return true;
15
        else if(matrix[i][j]>target)
16
            j--;
17
        else
18
            i++;
19
    }
20
    return false;
21
}

3 从头到尾打印链表(06)

输入一个链表的头节点，从尾到头反过来返回每个节点的值（用数组返回）。

1
//输入：head = [1,3,2]  输出：[2,3,1]
2
//1 反转链表并求长度 2 赋值
3
public int[] reversePrint(ListNode head) {
4
    int size = 0;
5
    ListNode pre = null, cur = head;
6
    while (cur != null) {
7
        size++;
8
        ListNode temp = cur.next;
9
        cur.next = pre;
10
        pre = cur;
11
        cur = temp;
12
    }
13
    int i = 0;
14
    int[] res = new int[size];
15
    while (pre != null) {
16
        res[i++] = pre.val;
17
        pre = pre.next;
18
    }
19
    return res;
20
}
21
//也可以将链表值压入栈中 再依次取出

4 重建二叉树(07)

输入某二叉树的前序遍历和中序遍历的结果，请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字

1
// Input:前序遍历 preorder = [3,9,20,15,7] 中序遍历 inorder = [9,3,15,20,7]  
2
//map中存放中序遍历的值的索引位置，便于找到前序遍历中根节点所在位置
3
HashMap<Integer, Integer> map = new HashMap<>();
4
public TreeNode buildTree(int[] preorder, int[] inorder) {
5
    for (int i = 0; i < inorder.length; i++)
6
        map.put(inorder[i], i);
7
    return buildTree(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);
8
}
9
public TreeNode buildTree(int[] preorder, int pre_L, int pre_R, int[] inorder, int in_L, int in_R) {//左闭右闭区间
10
    //递归终止条件
11
    if (pre_L > pre_R) return null;
12
    TreeNode root = new TreeNode(preorder[pre_L]);
13
    int pivot = map.get(preorder[pre_L]);//找到中序遍历中根节点的位置
14
    int left_size = pivot - in_L;//左子树的大小
15
    root.left = buildTree(preorder, pre_L + 1, pre_L + left_size, inorder, in_L, pivot - 1);
16
    root.right = buildTree(preorder, pre_L + left_size + 1, pre_R, inorder, pivot + 1, in_R);
17
    return root;
18
}
19
//难点，确定左右子树的边界

5 两个栈实现一个队列(09)

用两个栈实现一个队列。队列的声明如下，请实现它的两个函数 appendTail 和 deleteHead ，分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素，deleteHead 操作返回 -1 )

1
//队尾插入元素时，在A中直接插入元素 
2
//删除队头元素时，判断B中是否含有元素，有则直接删除，没有将A中元素插入到B中再删
3
Stack<Integer>  A ;
4
Stack<Integer> B ;
5
public CQueue() {
6
    A = new Stack<>();//先
7
    B= new Stack<>();//后
8
}
9
public void appendTail(int value) {//插入时要确保A中没有元素
10
    A.push(value);                
11
}
12
public int deleteHead() {
13
    if(!B.isEmpty())//B不为空
14
        return B.pop();
15
    while(!A.isEmpty())//B为空，将A中的元素移入B中
16
        B.push(A.pop());
17
    return B.isEmpty()?-1: B.pop();
18
}
19
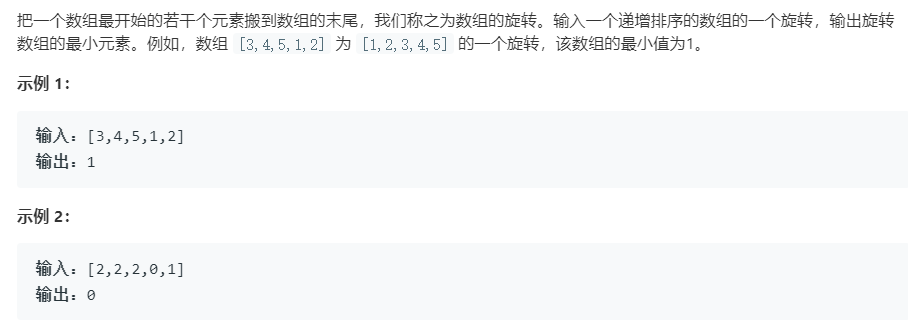
//另一种思路：(栈底为队头，栈头为队尾，目的要将两者颠倒)用A做主栈，B做辅助栈，队尾插入时:先判断A中是否含有元素，有则移入B中，插入当前元素后再将B中元素移入到A中；删除队头元素则直接删除A的栈顶元素

6 旋转数组的最小数字

1
class Solution {
2
    //数组默认递增，经过旋转
3
    //两种思路:1 直接遍历，找出最小数字 时间复杂度为O(N)
4
    /**2 二分查找思想，利用mid与right两个值做判断，时间复杂度(Log N)
5
    **/
6
    public int minArray(int[] numbers) {
7
            int left = 0,right=numbers.length-1;
8
            while(left<right){
9
                int mid =left+(right-left)/2;
10
                if(numbers[mid]>numbers[right])//中间比右边大，最小值在右半部分
11
                    left=mid+1;
12
                else if(numbers[mid]<numbers[right])//中间比右边小，近似有序，左半部分，可能包含mid
13
                    //[3,1,2]
14
                    right=mid;
15
                else right--;//相等则去除重复
16
            }
17
            return numbers[left];
18
    }
19
}

7 矩阵路径(12)

1
//深度优先搜索+回溯  
2
public boolean exist(char[][] board, String word) {
3
        char[] words = word.toCharArray();
4
        int row =  board.length,col =  board[0].length;
5
        for(int i=0;i<row;i++)
6
            for(int j=0;j<col;j++){
7
              if(dfs(board,i,j,words,0))
8
                  return true;
9
            }
10
        return false;
11
    }
12
    public  boolean dfs(char[][] board,int i,int j,char[] words,int k){
13
        //终止条件:数组越界或值不相等时，返回false
14
        if(i<0||j<0||i>=board.length||j>=board[0].length||board[i][j]!=words[k])
15
            return false;
16
        //值相等且已经找到最后一个值时，即已经找到一条路径
17
        if(k==words.length-1)
18
            return true;
19
        //遍历每个路径后将其标记，遍历后需要返回访问其状态，回溯思想
20
        char tmp =board[i][j];
21
        board[i][j] = '.';
22
        boolean flag =  dfs(board,i+1,j,words,k+1)||dfs(board,i-1,j,words,k+1)|| 
23
                        dfs(board,i,j+1,words,k+1)|| dfs(board,i,j-1,words,k+1);
24
        board[i][j] = tmp;
25
        return flag;
26
    }

8 机器人运动范围(13)

1
//两种思路:DFS or BFS
2
//1 DFS
3
 class Solution {
4
        boolean[][] visited;//记录以访问过的点，避免重复访问
5
        public int movingCount(int m, int n, int k) {
6
            visited = new boolean[m][n];
7
            return dfs(m, n, k, 0, 0);
8
        }
9
        public int dfs(int m, int n, int k, int i, int j) {
10
            int sum = add(i) + add(j);
11
            if (i < 0 || i >= m || j < 0 || j >= n || visited[i][j] || sum > k)
12
                return 0;
13
            visited[i][j] = true;//记录访问点
14
            return dfs(m, n, k, i + 1, j) + dfs(m, n, k, i - 1, j)
15
                    + dfs(m, n, k, i, j - 1) + dfs(m, n, k, i, j + 1) + 1;
16
        }
17
        public int add(int n) {
18
            int sum = 0;
19
            while (n > 0) {
20
                sum += n % 10;
21
                n /= 10;
22
            }
23
            return sum;
24
        }
25
    }
1
//BFS,类似于层次遍历，借助队列实现
2
public int movingCount(int m, int n, int k) {
3
    Queue<int[]> queue = new LinkedList<>();
4
    queue.offer(new int[]{0, 0});
5
    int res = 0;
6
    boolean[][] visited = new boolean[m][n];
7
    while (queue.size() > 0) {
8
        int[] tmp = queue.poll();
9
        int i = tmp[0], j = tmp[1];
10
        int sum = add(i) + add(j);
11
        if (i < 0 || i >= m || j < 0 || j >= n || visited[i][j] || sum > k)
12
            continue;
13
        res++;
14
        visited[i][j] = true;
15
        queue.offer(new int[]{i + 1, j});//将当前位置的右边和下方的位置放入队列中
16
        queue.offer(new int[]{i, j + 1});
17
    }
18
    return res;
19
}

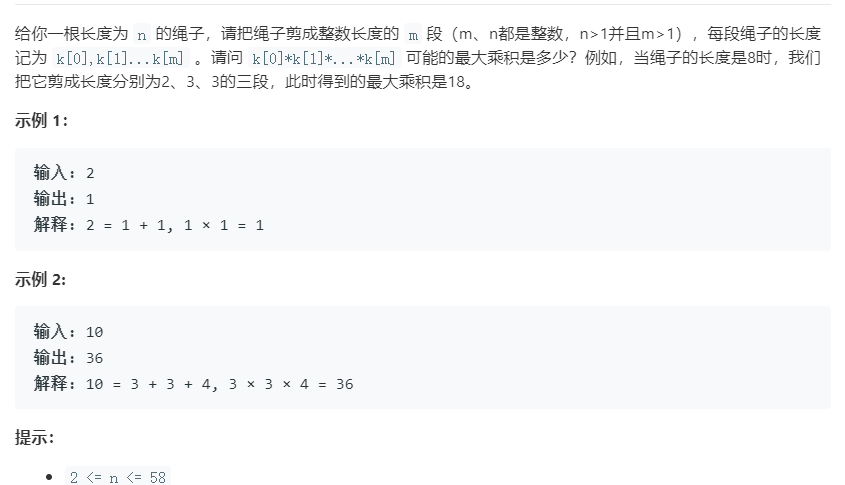
9 剪绳子(14)

1
//1 动态规划问题 时间:O(N2) 空间 O(N)
2
class Solution {
3
    public int cuttingRope(int n) {
4
        int [] dp =new int[n+1];//dp[i]为长度为i绳子的最大乘积
5
        dp[2]=1;
6
        for(int i =3;i<=n;i++){//从3开始遍历
7
            for(int j=1;j<=i-1;j++){//从长度为1-(i-1)的绳子开始切割比较
8
			   //求出当前长度为i的绳子的最大乘积
9
                //需要比较当前以长度j切割(j*(i-j))和j*dp[i-j]最大的一方
10
                //因为i-j长度的绳子的最大乘积不一定是i-j
11
                dp[i] = Math.max(dp[i],Math.max(j*(i-j),j*dp[i-j])); 
12
            }
13
        }
14
        return dp[n];
15
    }
16
}
1
/**2 贪心/数学思想
2
   *经数学验证，划分3可以比2的优先级高
3
   *令n=3k+b, k =n/3,b=b%3;
4
   *(1) b=0 最大乘积:Math.pow(3,k)
5
   *(2) b=1 ,1+3<2*2,最大乘积:3^(k-1)*4
6
   *(3) b=2,最大乘积:3^k*2 
7
**/ 
8
public int cuttingRope(int n) {
9
    if(n<=3)
10
        return n-1;
11
    int k=n/3,b=n%3;
12
    if(b==0)
13
        return (int)Math.pow(3,k);
14
    else if(b==1)
15
        return (int)Math.pow(3,k-1)*4;
16
    else
17
        return (int)Math.pow(3,k)*b;
18
}
19
//https://leetcode-cn.com/problems/jian-sheng-zi-lcof/solution/mian-shi-ti-14-i-jian-sheng-zi-tan-xin-si-xiang-by/
20
//https://leetcode-cn.com/problems/integer-break/solution/tan-xin-xuan-ze-xing-zhi-de-jian-dan-zheng-ming-py/

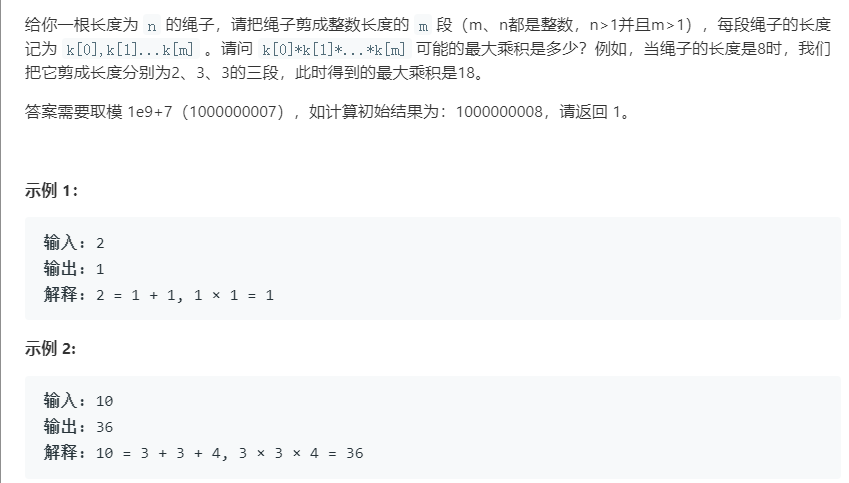
10 剪绳子II(14)

1
	/**关键点，求出3^(k-1),令res=3^(k-1)
2
    *令n=3k+b, k =n/3,b=b%3;
3
    *(1) b=0 最大乘积:res*3;
4
    *(2) b=1 ,1+3<2*2,最大乘积:res*4;
5
    *(3) b=2,最大乘积:res*6; 
6
    **/   
7
public int cuttingRope(int n) {
8
        if (n <= 3)
9
            return n - 1;
10
        int b = n % 3, k = n / 3 - 1, p = 1000000007;
11
        long res = 1, a = 3;
12
        while (k > 0) {//快速幂，求3^(k-1)
13
            if ((k & 1) == 1)
14
                res = (res * a) % p;
15
            a = (a * a) % p;
16
            k >>= 1;
17
        }
18
        if (b == 0)
19
            return (int) (res * 3 % p);
20
        else if (b == 1)
21
            return (int) (res * 4 % p);
22
        return (int) (res * 6 % p);
23
24
    }

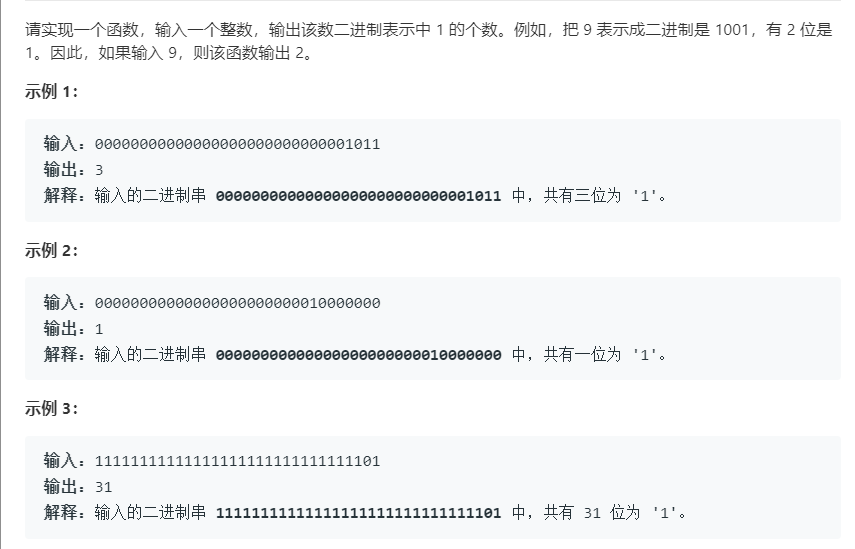
11 二进制中1的个数(15)

image-20200229203908344

1
public int hammingWeight(int n) {
2
    int res =0;
3
    while(n!=0){
4
      /** 法1 : n&1 依次判断n的每一位是否为1  
5
      if((n&1)==1)
6
            res++;
7
        n>>>=1;**/
8
        //法2 :  n&=(n-1)可消除n中最右边的1, 如 n=11010 n-1=11001 n&(n-1)=11000 最右边的1消除了
9
        res++;
10
        n&=(n-1);
11
    }
12
    return res;
13
}

12 数值的整数次方(16)

image-20200229205121960

1
//1 快速幂思想(递归)
2
//x^n =(x^n/2)^2 令 half_val = x^n/2
3
//n为偶数 half_val*half_val = x^n;
4
//n为奇数  half_val*half_val = x^(n-1),如n=5 x^5/2*x^5/2=x^4 ,此时 x^n=x*x^(n-1) =x*half_val*half_val
5
class Solution { 
6
    public double myPow(double x, int n) {
7
        if(n<0)
8
            x=1.0/x;
9
        return func(x,Math.abs(n));
10
    }
11
    public double func(double x,int n){
12
        if(n==0)
13
            return 1.0;
14
        double half_val =  func(x,n/2);
15
        if(n%2==0)
16
            return half_val*half_val;
17
        else
18
            return x*half_val*half_val;
19
    }
20
}
1
//2 迭代快速幂(位运算思想),将幂划为二进制表示，等于1的位置放入结果中
2
//2^13=2^8*2^4*2^1  13=1101
3
public double myPow(double x, int n) {
4
    long y = n;
5
    if (n < 0) {
6
        x = 1 / x;
7
        y = -y;
8
    }
9
    double res = 1.0;
10
    while (y > 0) {
11
        if ((y % 2) == 1)
12
            res *= x;
13
        x *= x;
14
        y >>= 1;
15
    }
16
    return res;
17
}

13 链表的倒数第k个节点(22)

1
//快慢指针法
2
   public ListNode getKthFromEnd(ListNode head, int k) {
3
        if(head==null||k==0)
4
            return head;
5
        ListNode low_node =head,fast_node = head;
6
        int cur=0;
7
        while(cur<k){
8
            fast_node=fast_node.next;
9
            cur++;
10
        }
11
        while(fast_node!=null){
12
            fast_node =fast_node.next;
13
            low_node =low_node.next;
14
        }
15
        return low_node;
16
    }

14 反转链表(24)

1
//遍历 或者递归  
2
public ListNode reverseList(ListNode head) {
3
          if(head==null||head.next==null) return head;
4
          /**  ListNode pre=null,cur=head;
5
            while(cur!=null){
6
                ListNode temp = cur.next;
7
                cur.next=pre ;
8
                pre= cur;
9
                cur= temp;
10
            } 
11
            return pre;**/
12
            ListNode pre =reverseList(head.next);
13
            head.next.next = head;
14
            head.next =null;
15
            return pre; 
16
17
    }

15 合并两个有序链表(25)

1
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
2
       if(l1==null)    return l2;
3
       if(l2 == null) return l1;
4
       ListNode head = new ListNode(0);
5
       ListNode cur =head;
6
       while(l1!=null&&l2!=null){
7
           if(l1.val<l2.val){
8
               cur.next =l1;
9
               cur =l1;
10
               l1=l1.next;
11
           }
12
           else{
13
               cur.next =l2;
14
               cur=l2;
15
               l2=l2.next;
16
           }
17
       }
18
       if(l1!=null) cur.next=l1;
19
       if(l2!=null) cur.next=l2;
20
       return head.next;
21
   }

16 树的子结构(26)

image-20200303212345624

1
//递归
2
    public boolean isSubStructure(TreeNode A, TreeNode B) {
3
            if(B==null||A==null)
4
                return false;
5
            if(B.left==null&&B.right==null&&B.val==A.val)
6
                return true;    
7
            if(B.val!=A.val) return isSubStructure(A.left,B)||isSubStructure(A.right,B);
8
            boolean match= true;
9
            if(B.left!=null)
10
               match&= isSub(A.left,B.left);
11
            if(B.right!=null)
12
               match&=  isSub(A.right,B.right);
13
            return match;
14
    }
15
    public boolean isSub(TreeNode A,TreeNode B){
16
        if(B==null||A==null)
17
                return false;
18
        if(B.left==null&&B.right==null&&B.val==A.val)
19
                return true;   
20
        if(B.val!=A.val)
21
                return false; 
22
                boolean match= true;
23
        if(B.left!=null)
24
            match&= isSub(A.left,B.left);
25
        if(B.right!=null)
26
            match&=  isSub(A.right,B.right);
27
        return match;
28
    }
1
//参考讨论区优化递归代码
2
 public boolean isSubStructure(TreeNode A, TreeNode B) {
3
            if(B==null||A==null)
4
                return false;
5
            return  isSub(A,B)||isSubStructure(A.left,B)||isSubStructure(A.right,B);
6
    }
7
    public boolean isSub(TreeNode A,TreeNode B){
8
        if(B==null)
9
                return true;
10
        if(A==null)
11
                return false;        
12
        return B.val==A.val&&isSub(A.left,B.left)&&isSub(A.right,B.right);
13
    }

17 二叉树的镜像(27)

image-20200229225637108

1
//1 递归(DFS) 有三种写法 对应先、中、后序遍历
2
class Solution {
3
    public TreeNode mirrorTree(TreeNode root) {
4
        //后序遍历写法
5
        if(root==null)//终止条件，即从叶子节点开始交换
6
            return null;
7
        TreeNode left =   mirrorTree(root.left);
8
        TreeNode right =  mirrorTree(root.right);
9
        root.left =right;
10
        root.right =left;
11
        return root;
12
    }
13
}
1
//2 迭代 层次遍历 BFS思想,借助队列
2
public TreeNode mirrorTree(TreeNode root) {
3
    if (root == null)
4
        return null;
5
    Queue<TreeNode> queue = new LinkedList<>();
6
    queue.offer(root);
7
    while (!queue.isEmpty()) {
8
        TreeNode cur_node = queue.poll();
9
        //交换 left和right
10
        TreeNode tmp = cur_node.left;
11
        cur_node.left = cur_node.right;
12
        cur_node.right = tmp;
13
        //cur_node的左右孩子入队列
14
        if (cur_node.left != null)
15
            queue.offer(cur_node.left);
16
        if (cur_node.right != null)
17
            queue.offer(cur_node.right);
18
    }
19
    return root;
20
}

18对称二叉树(28)

image-20200303221630135

1
//递归
2
    public boolean isSymmetric(TreeNode root) {
3
       return isMirror(root,root);
4
    }
5
    public boolean isMirror(TreeNode root1,TreeNode root2){
6
        if(root1==null&&root2==null)//两者都为空,说明遍历完成,返回true
7
            return true;
8
        if(root1==null||root2==null)//有一个为null,不符合要求
9
            return false;
10
        return root1.val==root2.val&&
11
               isMirror(root1.left,root2.right)&&
12
               isMirror(root1.right,root2.left);
13
    }
1
//BFS，层次遍历思想
2
  public boolean isSymmetric(TreeNode root) {
3
        if(root==null)
4
            return true;
5
        Queue<TreeNode> q =new LinkedList<>();
6
        q.offer(root.left);
7
        q.offer(root.right);
8
        while(!q.isEmpty()){
9
            TreeNode left_node = q.poll();
10
            TreeNode right_node =q.poll();
11
            if(left_node==null&&right_node==null)
12
                continue;
13
            if(left_node==null||right_node==null)
14
                return false;
15
            if(left_node.val!=right_node.val)
16
                return false;
17
            q.offer(left_node.left);
18
            q.offer(right_node.right);
19
            q.offer(left_node.right);
20
            q.offer(right_node.left);
21
        }
22
        return true;
23
  }

19 螺旋矩阵(29)

1
 /**  	 1 2 3
2
         4 5 6
3
         7 8 9
4
         print: 1 2 3 6 9 8 7 4 5
5
 **/
6
public int[] spiralOrder(int[][] matrix) {
7
    if(matrix.length==0)
8
        return new int[0];
9
    int row = matrix.length,col = matrix[0].length;
10
    int left = 0,right= matrix[0].length-1,top = 0,down = matrix.length-1;
11
    //l->r->d->l->t 左右下左上
12
    int [] res =new int[row*col];
13
    int index =0;
14
    while(true){
15
        for(int i =left;i<=right;i++)  
16
            res[index++]=matrix[top][i];//left ->right
17
        if(++top>down) break;
18
        for(int i =top;i<=down;i++)  
19
            res[index++]=matrix[i][right];//top ->down
20
        if(--right<left) break;
21
        for(int i =right;i>=left;i--)  
22
            res[index++]=matrix[down][i];//right->left 
23
        if(--down<top) break;
24
        for(int i =down;i>=top;i--)
25
            res[index++] =matrix[i][left];//down->top
26
        if(++left>right) break;
27
    }
28
    return res;
29
}

20 栈的压入、弹出序列(31)

image-20200304222829076

1
//两次遍历  
2
public boolean validateStackSequences(int[] pushed, int[] popped) {
3
        if(pushed.length==0) return true;
4
        Stack<Integer> stack = new Stack<>();
5
        int pop = 0;
6
        //第一次匹配
7
        for(int i=0;i<pushed.length;){
8
            if(!stack.isEmpty()&&popped[pop]==stack.peek()){
9
                //挨个匹配出栈序列，若与栈顶元素相同，元素出栈
10
                stack.pop();
11
                pop++;//向后寻找
12
            }
13
            else {//不相等，元素继续入栈
14
                stack.push(pushed[i++]);
15
            }
16
        }
17
        //第二次匹配，栈不为空时，应判断未经匹配的出栈序列是否与进栈序列一致，不一致直接返回false
18
       while(!stack.isEmpty()){
19
            int top =stack.pop();
20
            if(top!=popped[pop]) return false;
21
            pop++;
22
        }
23
        return true;
24
    }
1
//一次遍历
2
 public boolean validateStackSequences(int[] pushed, int[] popped) {
3
        if(pushed.length==0) return true;
4
        Stack<Integer> stack = new Stack<>();
5
        int pop = 0;
6
        for(int i=0;i<pushed.length;i++){
7
            stack.push(pushed[i]);//先将元素入栈
8
            while(!stack.isEmpty()&&popped[pop]==stack.peek()){
9
                //每入一个元素都判断出栈序列与辅助栈栈顶元素是否匹配成功
10
                stack.pop();
11
                pop++;
12
            }
13
        }
14
        return stack.isEmpty();
15
 }

21 自上而下打印二叉树III(32)

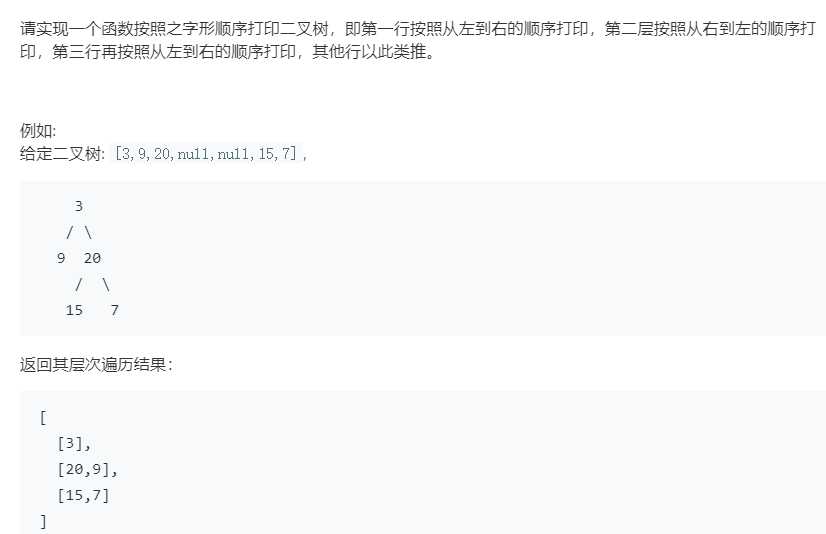
image-20200305214312757

1
class Solution {
2
    //借助双向队列
3
    //奇数层: 在队列尾依次取，队列头进（先左后右）
4
    //偶数层: 在队头取，队尾进(先右后左)
5
    public List<List<Integer>> levelOrder(TreeNode root) {
6
        List<List<Integer>> res = new ArrayList<>();
7
        if(root==null)  return res;
8
        Deque<TreeNode> q= new LinkedList<>();
9
        q.offer(root);
10
        int depth=1;
11
        while(!q.isEmpty()){
12
            int size = q.size();
13
            List<Integer> tmp =new ArrayList<>();
14
            while(size-->0){
15
                //奇层队尾取，偶层队头取
16
                TreeNode tmp_node = (depth%2==0?q.pollFirst():q.pollLast());
17
                tmp.add(tmp_node.val);
18
                if(depth%2==0){//偶数层:从右往左队尾进
19
                    if(tmp_node.right!=null) q.offerLast(tmp_node.right);
20
                    if(tmp_node.left!=null) q.offerLast(tmp_node.left);
21
                }
22
                else{ //奇数层：从左往右队头进
23
                    if(tmp_node.left!=null) q.offerFirst(tmp_node.left);
24
                    if(tmp_node.right!=null) q.offerFirst(tmp_node.right);
25
                }
26
            }
27
            depth++;
28
            res.add(tmp);
29
        }
30
        return res;
31
    }
32
}

22 二叉搜索树与双向链表(36)

题目描述：输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。

1
//递归,中序遍历思想
2
class Solution {
3
    Node  head=null,tail =null;//head:记录链表头部，tail:记录链表尾部
4
    Node pre =null;//记录中序遍历前一次访问的节点，以便处理当前节点的left和前一个节点right
5
    public Node treeToDoublyList(Node root) {
6
        if(root==null)
7
            return root;
8
        inorder(root);
9
        head.left = tail;//头尾结点处理
10
        tail.right = head;
11
        return head;
12
    }
13
    public void inorder(Node root){
14
        if(root ==null) return;
15
        inorder(root.left);
16
        if(head==null)  head = root;//处理头节点
17
        else{
18
            pre.right=root;
19
            root.left =pre;
20
        }
21
        pre =root;
22
        tail =root;//遍历到最后一步，tail指向最后一个节点
23
        inorder(root.right);
24
    }
25
}
1
//迭代思想，利用栈来处理中序遍历
2
public Node treeToDoublyList(Node root) {
3
    if (root == null)
4
        return root;
5
    Node head = null, tail = null;
6
    Node cur = root, pre = null;
7
    Stack<Node> stack = new Stack<>();
8
    while (!stack.isEmpty() || cur != null) {
9
        while (cur != null) {
10
            stack.push(cur);
11
            cur = cur.left;
12
        }
13
        cur = stack.pop();
14
        tail = cur;
15
        if (head == null) {
16
            head = cur;
17
        } else {
18
            pre.right = cur;
19
            cur.left = pre;
20
        }
21
        pre = cur;
22
        cur = cur.right;
23
    }
24
    head.left = tail;
25
    tail.right = head;
26
    return head;
27
}

23 字符串排列(38)

1
/**输入：s = "abc"
2
输出：["abc","acb","bac","bca","cab","cba"]
3
**/
4
//全排列思想，回溯，set去重
5
Set<String> res =new HashSet<>();
6
public String[] permutation(String s) {
7
    boolean[] visited = new boolean[s.length()];
8
    String tmp ="";
9
    dfs(s, 0,tmp, visited);
10
    return res.toArray(new String[res.size()]);
11
}
12
public void dfs(String s , int index,String tmp, boolean[] visited) {
13
    if (index == s.length()) {
14
        res.add(new String(tmp));
15
        return ;
16
    }
17
    for (int i = 0; i < s.length(); i++) {
18
        if (!visited[i]) {
19
            visited[i] = true;
20
            tmp+=s.charAt(i);
21
            dfs(s, index + 1, tmp, visited);
22
            visited[i] = false;
23
            tmp =tmp.substring(0,tmp.length()-1);
24
        }
25
    }
26
}

24 二叉搜索树的后序遍历

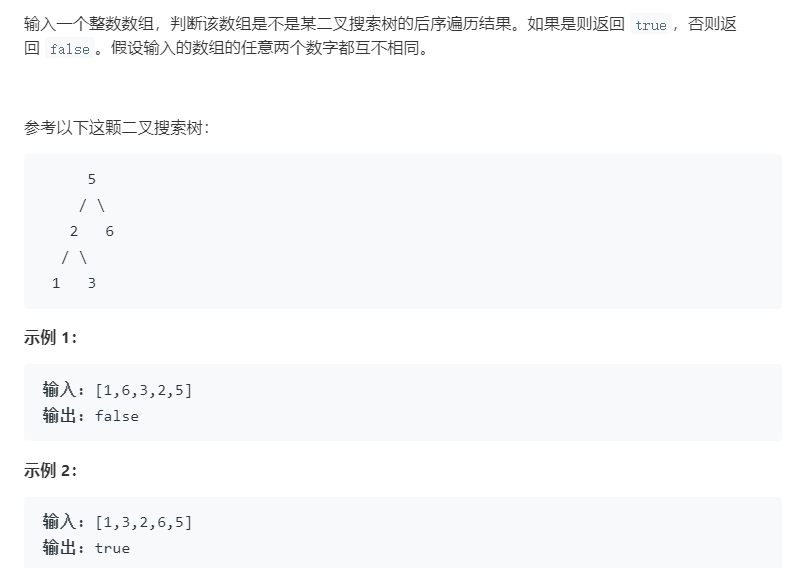
image-20200314214937071

1
//思路:右>根>左
2
public boolean verifyPostorder(int[] postorder) {
3
    if(postorder.length<=2)
4
        return true;
5
    return verify(postorder,0,postorder.length-1);
6
}
7
public boolean verify(int[] postorder,int start,int end){
8
    if(start>=end)
9
        return true;
10
    int cur = start;
11
    while(cur<=end&&postorder[cur]<postorder[end])
12
        //找到第一个大于根的位置,[cur,end]位置的所有值为右子树的值
13
        cur++;
14
    for(int i=cur;i<=end;i++){
15
        if(postorder[i]<postorder[end]) //右子树中出现小于根节点的值 false
16
            return false;
17
    }
18
    return verify(postorder,start,cur-1)&&verify(postorder,cur,end-1);//左子树&&右子树
19
}

25 二叉树的最近公共祖先(68)

1
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
2
    if(root==null||root==p||root==q)
3
        return root;
4
    TreeNode left = lowestCommonAncestor(root.left,p,q);
5
    TreeNode right = lowestCommonAncestor(root.right,p,q);
6
    if(left==null)//不在左子树中，即在右子树中
7
        return right;
8
    if(right==null)//不在右子树即在左子树
9
        return left;
10
    return root;//左右皆有，根节点为最近公共祖先
11
}
-------------未完待续-------------