今天写了剑指offer上面试题14,剪绳子题目,需要用到大数取余算法,特写下这篇文章以学习大数求余算法
[toc]
题目描述:
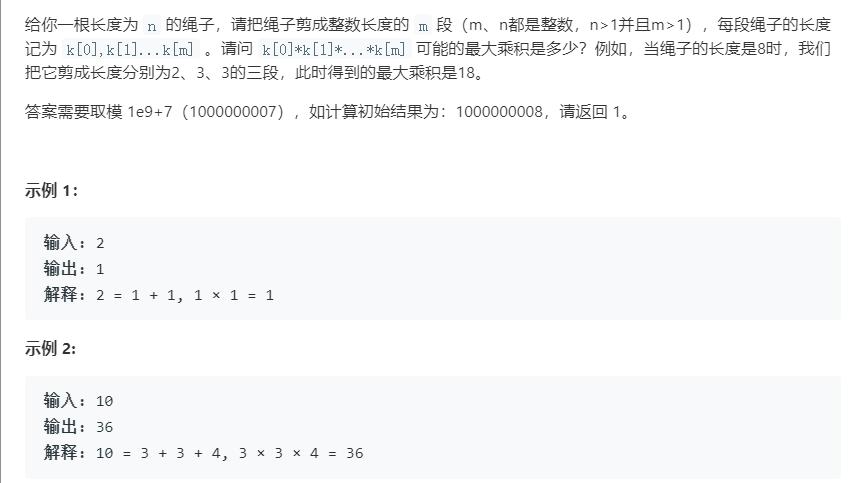
其中:
1 大数取余方法
整数求余满足的性质:
(1) 循环求余
依次求x^1,x^2,…x^n-1对p得余数,使得每一个余数均在可保存得范围内
1 | //x^n%p |
2 | public int remainder(int x,int n,int p){ |
3 | int res=1; |
4 | for(int i=0;i<n;i++){ |
5 | res =(res*x)%p; |
6 | } |
7 | return res; |
8 | } |
(2)快速幂
求a ^ b,快速幂的基本思路:
1)当b是奇数时,那么有 a^b = a * a^(b-1)
2)当b是偶数时,那么有 a^b = a^(b/2) * a^(b/2)
再根据模运算得性质a * a^(b-1)
1 | //递归写法 |
2 | public int remainder(int a ,int b,int p){ |
3 | if(b==0) |
4 | return 1; |
5 | else if(b%2==1)//奇数 |
6 | return a*remainder(a,b-1,p)%m; |
7 | else{ |
8 | int tmp = remainder(a,b/2,p)%m; |
9 | return (tmp*tmp)%m; |
10 | } |
11 | } |
1 | //非递归写法,位运算思想 |
2 | /**将b写成二进制,如2^13=2^8*2^4*2^1,13=1101 |
3 | *循环判断b末尾是否是1,是1,res*=b |
4 | * a=a*a,b右移一位 |
5 | *直到b<=0 |
6 | **/ |
7 | //PS:当a b p过大时,要将res和a设为long |
8 | public int remainder(int a ,int b,int p){ |
9 | int res= 1; |
10 | while(b>0){ |
11 | if(b&1==1){//or b%2==1 |
12 | res=(res*a)%p; |
13 | } |
14 | a=(a*a)%p; |
15 | b>>=1; |
16 | } |
17 | return res; |
18 | } |
2 问题解答
1 | /**关键点,求出3^(k-1),令res=3^(k-1) |
2 | *令n=3k+b, k =n/3,b=b%3; |
3 | *(1) b=0 最大乘积:res*3; |
4 | *(2) b=1 ,1+3<2*2,最大乘积:res*4; |
5 | *(3) b=2,最大乘积:res*6; |
6 | **/ |
7 | public int cuttingRope(int n) { |
8 | if (n <= 3) |
9 | return n - 1; |
10 | int b = n % 3, k = n / 3 - 1, p = 1000000007; |
11 | long res = 1, a = 3; |
12 | while (k > 0) {//快速幂,求3^(k-1) |
13 | if ((k & 1) == 1) |
14 | res = (res * a) % p; |
15 | a = (a * a) % p; |
16 | k >>= 1; |
17 | } |
18 | if (b == 0) |
19 | return (int) (res * 3 % p); |
20 | else if (b == 1) |
21 | return (int) (res * 4 % p); |
22 | return (int) (res * 6 % p); |
23 | } |