码龙的成长之路

0%

排序算法的实现

发表于 更新于
本文字数： 2.9k 阅读时长 ≈ 3 分钟

记录数据结构中典型的排序算法

[TOC]

img

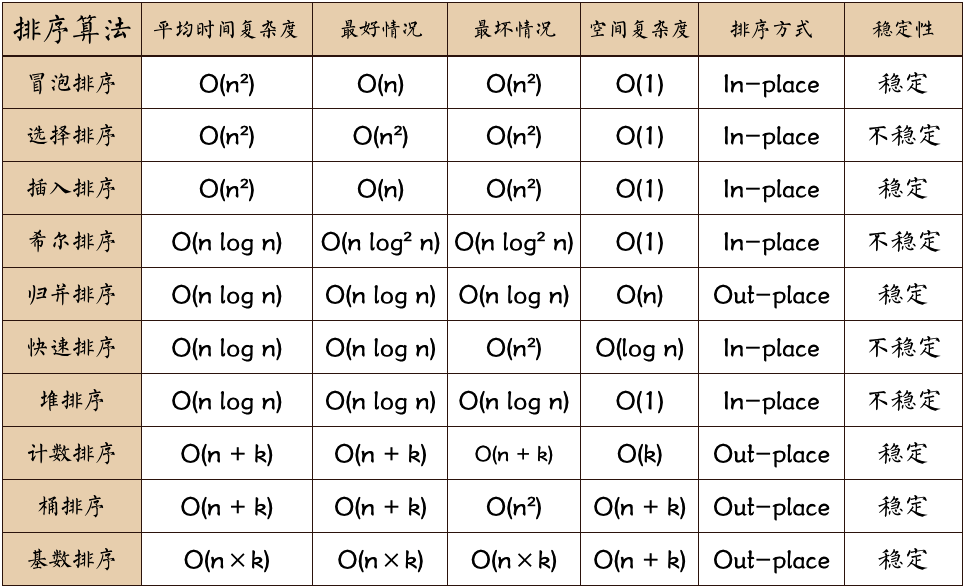
1 冒泡排序(稳定)

思想：每趟比较将当前数列未排序部分的最大的元素“沉”到数列末端，而小的元素会经由交换慢慢“浮”到数列的顶端。

1
public void sort(int[] arr) {
2
     for (int i = 0; i < arr.length; i++) {
3
         boolean flag = false;//记录是否发生交换，若一次遍历未发生交换，则数组已经有序
4
         for (int j = 0; j < arr.length - i - 1; j++) {//每次比较相邻的元素，较大者上浮
5
             if (arr[j + 1] < arr[j]) {
6
                 swap(arr, j, j + 1);
7
                 flag = true;
8
             }
9
         }
10
         if (!flag) break;
11
     }
12
 }

2 选择排序(不稳定)

思想：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕

1
public void sort(int[] arr) {
2
       for (int i = 0; i < arr.length - 1; i++) {
3
           int min_index = i;//每次循环找最小
4
           for (int j = i + 1; j < arr.length; j++) {
5
               if (arr[min_index] > arr[j])
6
                   min_index = j;
7
           }
8
           swap(arr, min_index, i);//交换
9
       }
10
   }

3 插入排序(不稳定)

思想：通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

1
public void sort(int[] arr) {
2
    for (int i = 1; i < arr.length; i++) {//[0,i-1]未有序序列
3
        int cur = arr[i], index = i - 1;
4
        while (index >= 0 && cur < arr[index]) {
5
            arr[index + 1] = arr[index];
6
            index--;
7
        }
8
        arr[index + 1] = cur;
9
    }
10
}

4 快速排序(不稳定)

思想：通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

记当前值为a,从右边找出比a小的元素，左边找到比a大的元素，交换，直到左右两索引相遇，此时，a左边值均小于a,右边均大于a,递归的执行

1
public void sort(int[] arr, int begin, int end) {
2
        if (begin >= end) return;//递归结束条件
3
        int cur = arr[begin];
4
        int i = begin, j = end;
5
        while (i < j) {
6
            while (i < j && arr[j] >= cur) j--;//右边找小于cur的
7
            while (i < j && arr[i] <= cur) i++;//左边找大于cur的
8
            if (i > j) break;//若当前i>j直接break
9
            swap(arr, i, j);//交换
10
        }
11
        arr[i] = cur;//将当前值(基准)移到i中
12
        sort(arr, begin, i - 1);//递归左半部分
13
        sort(arr, i + 1, end);//递归右半部分
14
    }

5 归并排序(稳定)

思想：分治n->n/2->…->1,再依次归并

1
 private void sort(int[] arr, int left, int right) {
2
        if (left < right) {
3
            int mid = left + (right - left) / 2;//分治
4
            sort(arr, left, mid);//处理[left,mid]
5
            sort(arr, mid + 1, right);//处理[mid+1,right]
6
            merge(arr, left, mid, right);//归并核心
7
        }
8
9
    }
10
//将[left,mid]和[mid+1,right]两个区间的数进行合并,利用temp数组存储合并后的结果
11
//将归并后的结果依次放到原数组的[left,right]位置
12
private void merge(int[] arr, int left, int mid, int right) {
13
    int[] temp = new int[right - left + 1];
14
    int i = left, j = mid + 1, index = 0;
15
    while (i <= mid && j <= right) {
16
        if (arr[i] <= arr[j]) {
17
            temp[index++] = arr[i++];
18
        } else {
19
            temp[index++] = arr[j++];
20
        }
21
    }
22
    while (i <= mid)
23
        temp[index++] = arr[i++];
24
    while (j <= right)
25
        temp[index++] = arr[j++];
26
    for (int k = 0; k < temp.length; k++)
27
        arr[left + k] = temp[k];//结果要与原数组[left，right]位置对应
28
}

6 堆排序(不稳定)

思想: 三步：1 建初始堆(大\小根堆) 2交换 3 调整堆

1
/** 1 建初始堆(大根堆)
2
* 	2 交换arr[0]和arr[i]
3
* 	3 调整堆
4
**/
5
private void sort(int[] arr) {
6
    int begin = (arr.length - 2) / 2;
7
    for (int i = begin; i >= 0; i--)//init heap
8
        adjust_heap(arr, i, arr.length);
9
    for (int i = arr.length - 1; i >= 0; i--) {
10
        swap(arr, i, 0);//swap
11
        adjust_heap(arr, 0, i);//adjust_heap
12
    }
13
}
14
private void adjust_heap(int[] arr, int begin, int length) {
15
    int temp = arr[begin];
16
    for (int i = 2 * begin + 1; i < length; i = 2 * i + 1) {
17
        if (i + 1 < length && arr[i + 1] > arr[i])
18
            i++;
19
        if (arr[i] <= temp) break;
20
        arr[begin] = arr[i];
21
        begin = i;
22
    }
23
    arr[begin] = temp;
24
}
-------------未完待续-------------