与LeetCode的相爱相杀,在解题中找到编程的乐趣,记录解题思路与你共同探讨;
Ps:Num+数字为LeetCode中相应题目编号
用回溯法解决问题三部曲:
- 画递归树
- 对递归树编码
- 找出终止条件,回溯
[toc]
一 二叉树类
Num 113:路径总和
1 |
|
2 |
|
3 |
|
4 | class Solution { |
5 | List<List<Integer>> ans_path = new ArrayList<>(); |
6 | List<Integer> node_path = new ArrayList<>(); |
7 | public List<List<Integer>> pathSum(TreeNode root, int sum) { |
8 | path_sum(root,sum); |
9 | return ans_path; |
10 | } |
11 | |
12 | public void path_sum(TreeNode root,int sum){ |
13 | if(root==null) |
14 | return ; |
15 | node_path.add(root.val); |
16 | if(root.left==null&&root.right==null){ |
17 | if(sum==root.val){ |
18 | ans_path.add(new ArrayList<>(node_path)); |
19 | } |
20 | } |
21 | sum-=root.val; |
22 | if(root.left!=null) |
23 | path_sum(root.left,sum); |
24 | if(root.right!=null) |
25 | path_sum(root.right,sum); |
26 | node_path.remove(node_path.size()-1); |
27 | } |
28 | } |
Num 129:根节点到叶子节点之和
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 | class Solution { |
14 | int ans = 0; |
15 | public int sumNumbers(TreeNode root) { |
16 | sumNumber(root,0); |
17 | return ans; |
18 | } |
19 | |
20 | public void sumNumber(TreeNode root,int sum){ |
21 | if(root==null) |
22 | return ; |
23 | if(root.left==null&&root.right==null){ |
24 | ans += 10*sum+root.val; |
25 | } |
26 | sumNumber(root.left,10*sum+root.val); |
27 | sumNumber(root.right,10*sum+root.val); |
28 | } |
29 | } |
Num 701: 二叉搜索树的插入操作
1 | class Solution { |
2 | |
3 | public TreeNode insertIntoBST(TreeNode root, int val) { |
4 | TreeNode cur = root, p = root; |
5 | while (cur != null) { |
6 | p = cur; |
7 | if (cur.val < val) |
8 | cur = cur.right; |
9 | else |
10 | cur = cur.left; |
11 | } |
12 | TreeNode new_code = new TreeNode(val); |
13 | if (p.val < val) |
14 | p.right = new_code; |
15 | else |
16 | p.left = new_code; |
17 | return root; |
18 | } |
19 | |
20 | public TreeNode insertIntoBST(TreeNode root, int val) { |
21 | if (root == null) |
22 | return new TreeNode(val); |
23 | if (root.val > val) |
24 | root.left = insertIntoBST(root.left, val); |
25 | else |
26 | root.right = insertIntoBST(root.right, val); |
27 | return root; |
28 | } |
29 | } |
Num230 :二叉搜索树的第k小个元素
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 | class Solution { |
11 | int ans =0,count=0; |
12 | public int kthSmallest(TreeNode root, int k) { |
13 | kthSmallests(root,k); |
14 | return ans; |
15 | } |
16 | |
17 | public void kthSmallests(TreeNode root,int k){ |
18 | if(root ==null) |
19 | return ; |
20 | kthSmallests(root.left,k); |
21 | if(++count==k){ |
22 | ans = root.val; |
23 | return; |
24 | } |
25 | kthSmallests(root.right,k); |
26 | } |
27 | } |
Num 687: 最大同值路径
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 | class Solution { |
9 | |
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 | int max = 0; |
16 | public int longestUnivaluePath(TreeNode root) { |
17 | longestUnivaluePaths(root); |
18 | return max; |
19 | } |
20 | public int longestUnivaluePaths(TreeNode root){ |
21 | if(root==null) |
22 | return 0; |
23 | int left = longestUnivaluePaths(root.left); |
24 | int right = longestUnivaluePaths(root.right); |
25 | if(root.left!=null&&root.val==root.left.val) |
26 | left= left + 1; |
27 | else left = 0; |
28 | if(root.right!=null&&root.val==root.right.val) |
29 | right=right+1; |
30 | else right = 0; |
31 | max = Math.max(max,left+right); |
32 | return Math.max(left,right); |
33 | } |
34 | } |
Num124 二叉树最大路径和
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 | class Solution { |
11 | |
12 | |
13 | int ans = Integer.MIN_VALUE; |
14 | public int maxPathSum(TreeNode root) { |
15 | maxPathSums(root); |
16 | return ans; |
17 | } |
18 | public int maxPathSums(TreeNode root){ |
19 | if(root==null) |
20 | return 0; |
21 | int left_val = Math.max(maxPathSums(root.left),0); |
22 | int right_val =Math.max(maxPathSums(root.right),0); |
23 | ans =Math.max(root.val+left_val+right_val,ans); |
24 | return root.val+Math.max(left_val,right_val); |
25 | } |
26 | } |
二 链表类
Num148:链表排序
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 | class Solution { |
7 | |
8 | public ListNode sortList(ListNode head) { |
9 | if (head == null || head.next == null) |
10 | return head; |
11 | ListNode mid_node = get_mid_node(head); |
12 | ListNode right_head = mid_node.next; |
13 | mid_node.next = null; |
14 | return merge_List(sortList(head), sortList(right_head)); |
15 | } |
16 | public ListNode get_mid_node(ListNode head) { |
17 | if (head == null || head.next == null) |
18 | return head; |
19 | ListNode low_node = head, fast_node = head; |
20 | while (fast_node.next != null && fast_node.next.next != null) { |
21 | low_node = low_node.next; |
22 | fast_node = fast_node.next.next; |
23 | } |
24 | return low_node; |
25 | } |
26 | public ListNode merge_List(ListNode p, ListNode q) { |
27 | ListNode cur_p = p, cur_q = q, head; |
28 | if (p.val < q.val) { |
29 | head = p; |
30 | cur_p = cur_p.next; |
31 | } else { |
32 | head = q; |
33 | cur_q = cur_q.next; |
34 | } |
35 | ListNode cur = head; |
36 | while (cur_q != null && cur_p != null) { |
37 | if (cur_q.val < cur_p.val) { |
38 | cur.next = cur_q; |
39 | cur_q = cur_q.next; |
40 | cur = cur.next; |
41 | } else { |
42 | cur.next = cur_p; |
43 | cur_p = cur_p.next; |
44 | cur = cur.next; |
45 | } |
46 | } |
47 | if (cur_p != null) |
48 | cur.next = cur_p; |
49 | if (cur_q != null) |
50 | cur.next = cur_q; |
51 | return head; |
52 | } |
53 | } |
Num 92:反转部分链表
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 | class Solution { |
7 | public ListNode reverseBetween(ListNode head, int m, int n) { |
8 | ListNode root = new ListNode(0); |
9 | ListNode cur = head,root_cur = root; |
10 | int index = 1; |
11 | while(index!=m){ |
12 | root_cur.next = cur; |
13 | root_cur=root_cur.next; |
14 | cur=cur.next; |
15 | index++; |
16 | } |
17 | ListNode temp = cur; |
18 | root_cur.next=null; |
19 | |
20 | while(index<=n){ |
21 | head = cur.next; |
22 | cur.next=root_cur.next; |
23 | root_cur.next =cur; |
24 | cur = head; |
25 | index++; |
26 | } |
27 | root_cur = temp; |
28 | if(cur!=null) |
29 | root_cur.next = c; |
30 | return root.next; |
31 | } |
32 | } |
Num61: 旋转链表
1 |
|
2 |
|
3 |
|
4 |
|
5 | class Solution { |
6 | |
7 |
|
8 |
|
9 |
|
10 | public ListNode rotateRight(ListNode head, int k) { |
11 | if(head==null) |
12 | return head; |
13 | int list_size = 0; |
14 | ListNode cur =head; |
15 | while(cur!=null){ |
16 | list_size++; |
17 | cur=cur.next; |
18 | } |
19 | k = k%list_size; |
20 | if(k==0) |
21 | return head; |
22 | ListNode k_node_last = find_last_k(head,k); |
23 | cur = k_node_last; |
24 | while(cur.next!=null){ |
25 | cur=cur.next; |
26 | } |
27 | while(head!=k_node_last){ |
28 | cur.next = head; |
29 | cur =head; |
30 | head= head.next; |
31 | } |
32 | cur.next =null; |
33 | return k_node_last; |
34 | } |
35 | public ListNode find_last_k(ListNode head,int k){ |
36 | ListNode cur=head,pre =head; |
37 | int index = 0; |
38 | while(++index<k){ |
39 | cur =cur.next; |
40 | } |
41 | while(cur.next!=null){ |
42 | pre =pre.next; |
43 | cur =cur.next; |
44 | } |
45 | return pre; |
46 | } |
Num 86 :分割链表
1 |
|
2 |
|
3 |
|
4 |
|
5 | class Solution { |
6 | |
7 |
|
8 |
|
9 |
|
10 |
|
11 | public ListNode partition(ListNode head, int x) { |
12 | if(head==null) |
13 | return head; |
14 | ListNode root = new ListNode(0); |
15 | ListNode cur = root,p = head,pre_p=head; |
16 | while(p!=null){ |
17 | if(p.val<x){ |
18 | ListNode temp =p.next; |
19 | if(p==head) |
20 | head = head.next; |
21 | else |
22 | pre_p.next = p.next; |
23 | cur.next = p; |
24 | cur = p; |
25 | p = temp; |
26 | } |
27 | else{ |
28 | pre_p = p; |
29 | p = p.next; |
30 | } |
31 | } |
32 | cur.next = head; |
33 | return root.next; |
34 | } |
35 | } |
Num114 二叉树转为链表
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 | class Solution { |
10 | public void flatten(TreeNode root) { |
11 | while(root!=null){ |
12 | |
13 | if(root.left==null) |
14 | root=root.right; |
15 | else{ |
16 | TreeNode last_right_node = root.left; |
17 | while(last_right_node.right!=null) |
18 | last_right_node=last_right_node.right; |
19 | last_right_node.right = root.right; |
20 | root.right = root.left; |
21 | root.left = null; |
22 | root = root.right; |
23 | } |
24 | } |
25 | } |
26 | } |
27 |
|
28 |
|
29 |
|
三 数组类
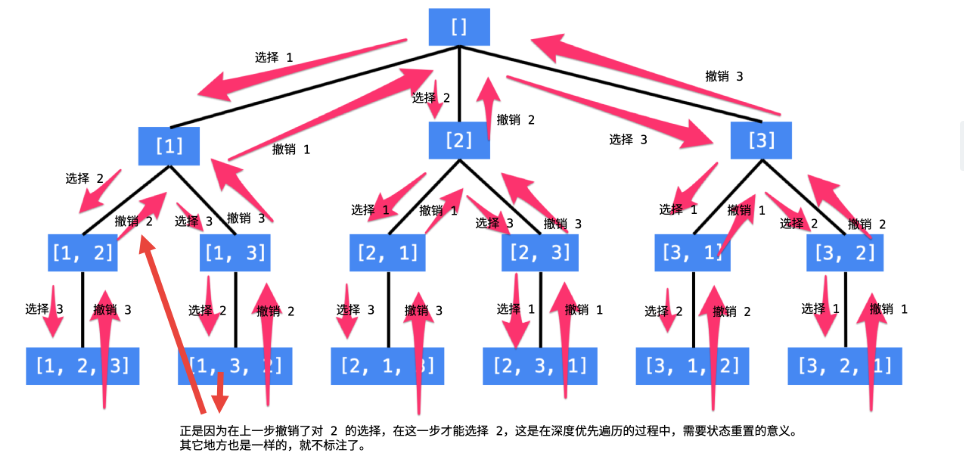
数组类题目和树类题目大部分皆可用回溯思想解决问题,特此总结了一套回溯题目的写法模板。
借用全排列示意图(来源:https://leetcode-cn.com/problems/permutations/solution/hui-su-suan-fa-python-dai-ma-java-dai-ma-by-liweiw/)
1 | List<List<Integer>> res = new HashSet<>(); |
2 | public List<List<Integer>> findSubsequences(int[] nums) { |
3 | List<Integer> tmp = new ArrayList<>(); |
4 | dfs(nums,0,tmp); |
5 | return new ArrayList<>(res); |
6 | } |
7 | public void dfs(int [] nums,int index,List<Integer> tmp){ |
8 | if(){ |
9 | return; |
10 | } |
11 | for(int i=index;i<nums.length;i++){ |
12 | tmp.add(nums[i]); |
13 | dfs(nums,index*,tmp); |
14 | tmp.remove(tmp.size()-1); |
15 | } |
16 | } |
Num560:和位k的子数组
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 | class Solution { |
7 | public int subarraySum(int[] nums, int k) { |
8 | HashMap<Integer,Integer> map = new HashMap<>(); |
9 | map.put(0,1); |
10 | int ans = 0,sum = 0; |
11 | for(int i=0;i<nums.length;i++){ |
12 | sum+=nums[i]; |
13 | |
14 | if(map.containsKey(sum-k)){ |
15 | ans+=map.get(sum-k); |
16 | } |
17 | map.put(sum,map.getOrDefault(sum,0)+1); |
18 | } |
19 | return ans; |
20 | } |
Num1 两数之和
1 |
|
2 |
|
3 |
|
4 | class Solution { |
5 | public int[] twoSum(int[] nums, int target) { |
6 | |
7 | HashMap<Integer,Integer> map = new HashMap<>(); |
8 | int[] res = new int[2]; |
9 | for(int i=0;i<nums.length;i++){ |
10 | if(map.containsKey(target-nums[i])){ |
11 | res[0]= i; |
12 | res[1] =map.get(target-nums[i]); |
13 | return res; |
14 | } |
15 | map.put(nums[i],i); |
16 | } |
17 | return res; |
18 | } |
19 | } |
Num15 三数之和
1 |
|
2 |
|
3 |
|
4 |
|
5 | class Solution { |
6 | public List<List<Integer>> threeSum(int[] nums) { |
7 | List<List<Integer>> res =new ArrayList<>(); |
8 | Arrays.sort(nums); |
9 | for(int k =0;k<nums.length-2;k++){ |
10 | if(nums[k]>0) break; |
11 | if(k>0&&nums[k]==nums[k-1]) continue; |
12 | int i = k+1,j= nums.length-1; |
13 | while(i<j){ |
14 | int sum = nums[k]+nums[i]+nums[j]; |
15 | if(sum==0){ |
16 | res.add(new ArrayList<>(Arrays.asList(nums[k], nums[i], nums[j]))); |
17 | while(i<j&&nums[i]==nums[++i]); |
18 | while(i<j&&nums[j]==nums[--j]); |
19 | } |
20 | else if(sum<0){ |
21 | while(i<j&&nums[i]==nums[++i]); |
22 | } |
23 | else |
24 | while(i<j&&nums[j]==nums[--j]); |
25 | } |
26 | } |
27 | return res; |
28 | } |
29 | } |
Num18:四数之和
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 | class Solution { |
8 | public List<List<Integer>> fourSum(int[] nums, int target) { |
9 | |
10 | List<List<Integer>> res =new ArrayList<>(); |
11 | Arrays.sort(nums); |
12 | HashSet<List<Integer>> set = new HashSet<>(); |
13 | for(int i = 0;i<nums.length-3;i++){ |
14 | for(int j = i+1;j<nums.length-2;j++){ |
15 | int left = j+1,right =nums.length-1; |
16 | while(left<right){ |
17 | int sum = nums[i]+nums[j]+nums[left]+nums[right]; |
18 | if(sum<target) left++; |
19 | else if(sum>target) right--; |
20 | else{ |
21 | set.add(Arrays.asList(nums[i],nums[j],nums[left],nums[right])); |
22 | left++;right--; |
23 | } |
24 | } |
25 | } |
26 | } |
27 | res.addAll(set); |
28 | return res; |
29 | } |
30 | } |
Num39 组合总和

1 |
|
2 |
|
3 | class Solution { |
4 | List<List<Integer>> res = new ArrayList<>(); |
5 | public List<List<Integer>> combinationSum(int[] candidates, int target) { |
6 | if(candidates.length==0) |
7 | return res; |
8 | List<Integer> temp = new ArrayList<>(); |
9 | dfs(temp,candidates,target,0); |
10 | return res; |
11 | } |
12 | public void dfs(List<Integer> temp, int [] candidates,int target,int begin){ |
13 | if(target<0) |
14 | return; |
15 | else if(target==0) |
16 | res.add(new ArrayList<>(temp)); |
17 | else{ |
18 | for(int i=begin;i<candidates.length;i++){ |
19 | temp.add(candidates[i]); |
20 | dfs(temp,candidates,target-candidates[i],i); |
21 | temp.remove(temp.size()-1); |
22 | } |
23 | } |
24 | } |
25 | } |
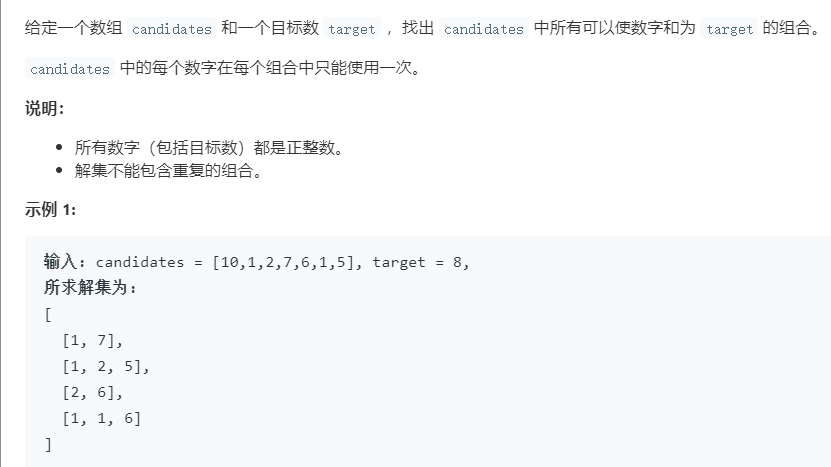
Num40 组合总和II
1 | class Solution { |
2 | List<List<Integer>> res = new ArrayList<>(); |
3 | public List<List<Integer>> combinationSum2(int[] candidates, int target) { |
4 | if(candidates.length==0) |
5 | return res; |
6 | List<Integer> temp = new ArrayList<>(); |
7 | Arrays.sort(candidates); |
8 | dfs(temp,candidates,target,0); |
9 | return res; |
10 | } |
11 | public void dfs(List<Integer> temp, int [] candidates,int target,int begin){ |
12 | if(target<0) |
13 | return; |
14 | else if(target==0) |
15 | res.add(new ArrayList<>(temp)); |
16 | else{ |
17 | for(int i=begin;i<candidates.length&&target-candidates[i]>=0;i++){ |
18 | |
19 | if(i!=begin&&candidates[i]==candidates[i-1]) continue; |
20 | temp.add(candidates[i]); |
21 | dfs(temp,candidates,target-candidates[i],i+1); |
22 | temp.remove(temp.size()-1); |
23 | } |
24 | } |
25 | } |
26 | } |
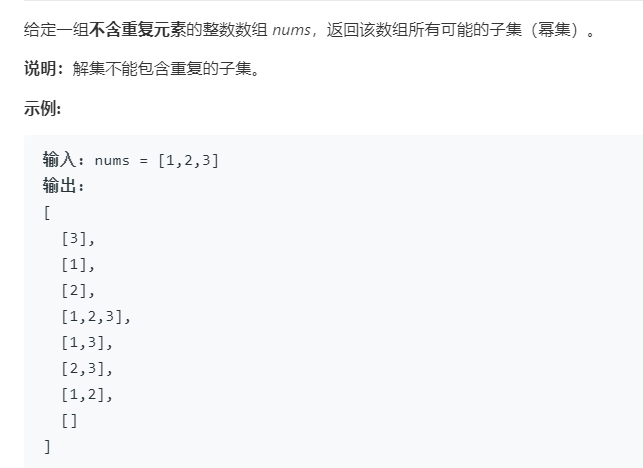
Num78 子集
1 |
|
2 | class Solution { |
3 | List<List<Integer>> res = new ArrayList<>(); |
4 | public List<List<Integer>> subsets(int[] nums) { |
5 | if(nums.length==0) |
6 | return res; |
7 | List<Integer> temp = new ArrayList<>(); |
8 | res.add(new ArrayList<>(temp)); |
9 | dfs(temp,nums,0); |
10 | return res; |
11 | } |
12 | public void dfs(List<Integer>temp, int [] nums,int start){ |
13 | if(start==nums.length) |
14 | return; |
15 | for(int i=start;i<nums.length;i++){ |
16 | temp.add(nums[i]); |
17 | res.add(new ArrayList<>(temp)); |
18 | dfs(temp,nums,i+1); |
19 | temp.remove(temp.size()-1); |
20 | } |
21 | } |
22 | } |
1 |
|
2 |
|
3 |
|
4 |
|
5 | , |
6 | public List<List<Integer>> subsets(int[] nums) { |
7 | List<List<Integer>> ans = new ArrayList<>(); |
8 | ans.add(new ArrayList<>()); |
9 | for(int i =0;i<nums.length;i++){ |
10 | List<Integer> temp; |
11 | int len = ans.size(); |
12 | for(int j = 0;j<len;j++){ |
13 | temp = new ArrayList<>(ans.get(j)); |
14 | temp.add(nums[i]); |
15 | ans.add(new ArrayList<>(temp)); |
16 | } |
17 | } |
18 | return ans; |
19 | } |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 | private static ArrayList<ArrayList<Integer>> getSubset(ArrayList<Integer> list) { |
8 | if (list.size() > 0) { |
9 | ArrayList<ArrayList<Integer>> result = new ArrayList<>(); |
10 | for (int i = 1; i < Math.pow(2, list.size()); i++) { |
11 | ArrayList<Integer> temp = new ArrayList<>(); |
12 | int index = i; |
13 | for (int j = 0; j < list.size(); j++) { |
14 | if ((index & 1) == 1) { |
15 | temp.add(list.get(j)); |
16 | } |
17 | index >>= 1; |
18 | } |
19 | result.add(temp); |
20 | } |
21 | return result; |
22 | } else { |
23 | return null; |
24 | } |
25 | } |
Num491 递增子序列

1 |
|
2 | class Solution { |
3 | Set<List<Integer>> res = new HashSet<>(); |
4 | public List<List<Integer>> findSubsequences(int[] nums) { |
5 | List<Integer> tmp = new ArrayList<>(); |
6 | dfs(nums,0,tmp); |
7 | return new ArrayList<>(res); |
8 | } |
9 | public void dfs(int[] nums, int index, List<Integer> tmp) { |
10 | if (tmp.size() > 1) |
11 | res.add(new ArrayList<>(tmp)); |
12 | for (int i = index; i < nums.length; i++) { |
13 | if (!tmp.isEmpty() && nums[i] < tmp.get(tmp.size() - 1)) continue; |
14 | tmp.add(nums[i]); |
15 | dfs(nums, i + 1, tmp); |
16 | tmp.remove(tmp.size() - 1); |
17 | } |
18 | } |
19 | } |
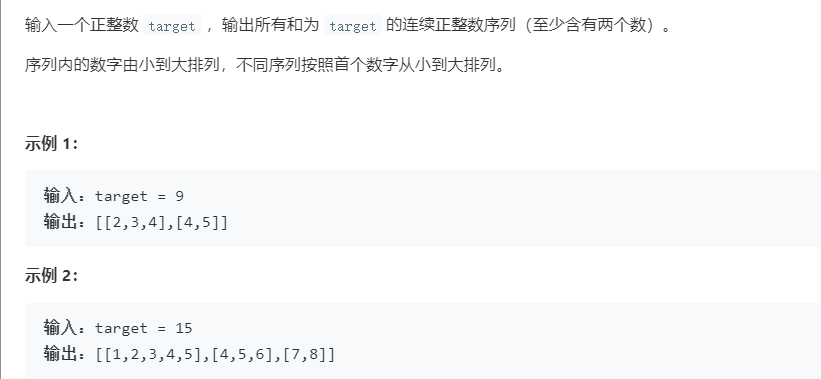
Num1543 和为s的连续正数序列
1 |
|
2 | public int[][] findContinuousSequence(int target) { |
3 | List<int []> ans = new ArrayList<>(); |
4 | int left = 1,right=1; |
5 | int sum = 0; |
6 | while (left <= target / 2) { |
7 | if (sum < target) { |
8 | sum += right; |
9 | right++; |
10 | } else if (sum > target) { |
11 | sum -= left; |
12 | left++; |
13 | } else { |
14 | int[] res = new int[right - left]; |
15 | for (int i = left; i < right; i++) { |
16 | res[i - left] = i; |
17 | } |
18 | ans.add(res); |
19 | sum -= left; |
20 | left++; |
21 | } |
22 | } |
23 | return ans.toArray(new int[ans.size()][]); |
24 | } |
Num698 划分k个相等的子集

1 |
|
2 |
|
3 |
|
4 | public boolean canPartitionKSubsets(int[] nums, int k) { |
5 | int sum = 0, max = 0; |
6 | for (int i = 0; i < nums.length; i++) { |
7 | sum += nums[i]; |
8 | max = Math.max(max, nums[i]); |
9 | } |
10 | if (sum % k != 0 || max > sum / k) |
11 | return false; |
12 | int target = sum / k; |
13 | |
14 | boolean[] visited = new boolean[nums.length]; |
15 | return dfs(nums, 0, 0, target, k, visited); |
16 | } |
17 | public boolean dfs(int[] nums, int start, int sum, int target, int k, boolean[] visited) { |
18 | if (k == 0) |
19 | return true; |
20 | if (sum == target) |
21 | return dfs(nums, 0, 0, target, k - 1, visited); |
22 | for (int i = start; i < nums.length; i++) { |
23 | if (!visited[i] && sum + nums[i] <= target) { |
24 | visited[i] = true; |
25 | if (dfs(nums, start + 1, sum + nums[i], target, k, visited)) |
26 | return true; |
27 | visited[i] = false; |
28 | } |
29 | } |
30 | return false; |
31 | } |
Num137 只出现一次的数字II
算例:
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 | public int singleNumber(int[] nums) { |
8 | int ans = 0; |
9 | for(int i=0;i<32;i++){ |
10 | int cnt = 0; |
11 | for(int j=0;j<nums.length;j++){ |
12 | cnt += (nums[j]>>>i&1)==1?1:0; |
13 | } |
14 | if(cnt%3!=0) |
15 | ans=ans|1<<i; |
16 | } |
17 | return ans; |
18 | } |
1 |
|
2 | public int singleNumber(int[] nums) { |
3 | int one=0,two=0,three=0; |
4 | for(int num:nums){ |
5 | |
6 | two|=one# |
7 | |
8 | one ^=num; |
9 | |
10 | three =one&two; |
11 | |
12 | one &=~three; |
13 | two &=~three; |
14 | } |
15 | return one; |
16 | } |
四 字符串类
Num 3 无重复字符的最长子串
1 |
|
2 |
|
3 |
|
4 |
|
5 | class Solution { |
6 | |
7 | public int lengthOfLongestSubstring(String s) { |
8 | HashMap<Character,Integer> map =new HashMap<>(); |
9 | int res = 0; |
10 | for(int i =0,left=0;i<s.length();i++){ |
11 | if(map.containsKey(s.charAt(i))){ |
12 | left = Math.max(map.get(s.charAt(i)),left); |
13 | } |
14 | res = Math.max(res,i-left+1); |
15 | map.put(s.charAt(i),i+1); |
16 | } |
17 | return res; |
18 | } |
19 | } |
Num42 最长有效括号

1 |
|
2 | public int longestValidParentheses(String s) { |
3 | Stack<Integer> stack = new Stack<>(); |
4 | List<Integer> list =new ArrayList<>(); |
5 | for (int i = 0; i < s.length(); i++) { |
6 | if (s.charAt(i) == ')') { |
7 | if (!stack.isEmpty()) { |
8 | list.add(stack.peek()); |
9 | list.add(i); |
10 | stack.pop(); |
11 | } |
12 | } else{ |
13 | stack.add(i); |
14 | } |
15 | } |
16 | Collections.sort(list); |
17 | |
18 | int res = 0, tmp = 0; |
19 | for (int i = 1; i < list.size(); i++) { |
20 | if (list.get(i) - list.get(i - 1) == 1) { |
21 | if (tmp == 0) |
22 | tmp++; |
23 | tmp++; |
24 | |
25 | } else { |
26 | res = Math.max(res, tmp); |
27 | tmp = 0; |
28 | } |
29 | } |
30 | res = Math.max(res, tmp); |
31 | return res; |
32 | } |
1 |
|
2 | public int longestValidParentheses(String s) { |
3 | int res = 0; |
4 | Stack<Integer> stack = new Stack<>(); |
5 | stack.push(-1); |
6 | for (int i = 0; i < s.length(); i++) { |
7 | if (s.charAt(i) == '(') |
8 | stack.push(i); |
9 | else { |
10 | stack.pop(); |
11 | if (stack.isEmpty()) { |
12 | stack.push(i); |
13 | } else |
14 | |
15 | res = Math.max(res, i - stack.peek()); |
16 | } |
17 | } |
18 | return res; |
19 | } |
1 |
|
2 | public int longestValidParentheses(String s) { |
3 | int res = 0; |
4 | int[] dp = new int[s.length()]; |
5 | for (int i = 1; i < s.length(); i++) { |
6 | if (s.charAt(i) == ')') { |
7 | if (s.charAt(i - 1) == '(') { |
8 | dp[i] = (i >= 2 ? dp[i - 2] + 2 : 2); |
9 | } |
10 | |
11 | |
12 | else if (i - dp[i - 1] > 0 && s.charAt(i - dp[i - 1] - 1) == '(') { |
13 | |
14 | dp[i] = (i - dp[i - 1] > 1 ? dp[i - dp[i - 1] - 2] : 0) + dp[i - 1] + 2; |
15 | } |
16 | res = Math.max(dp[i], res); |
17 | } |
18 | } |
19 | return res; |
20 | } |
21 |
|
Num22 括号生成

1 |
|
2 | List<String> res = new ArrayList<>(); |
3 | public List<String> generateParenthesis(int n) { |
4 | String str=""; |
5 | dfs(n,0,0,str); |
6 | return res; |
7 | } |
8 | public void dfs(int n,int left,int right,String str){ |
9 | if(left==n&&right==n){ |
10 | res.add(str); |
11 | return; |
12 | } |
13 | if(left<right) |
14 | return; |
15 | if(left<n) |
16 | dfs(n,left+1,right,str+"("); |
17 | if(right<n) |
18 | dfs(n,left,right+1,str+")"); |
19 | } |








